3D specialization of vector class. More...
#include <geomc/linalg/vecdetail/Vec3.h>
Public Types | |
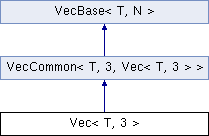
| using | base_t = detail::VecCommon<T,3,Vec<T,3>> |
| using | elem_t |
| The coordinate type of this object. | |
| using | point_t |
| The type of a point in this object's space. | |
| typedef Vec< T, N > | self_t |
| Self type. I.e., Vec<T,N> if a vector, Quat<T> if a quaternion. | |
Public Member Functions | |
| constexpr | Vec () |
| Construct vector with all elements set to 0. | |
| constexpr | Vec (const T v[3]) |
| Construct a vector with elements copied from the 3-element array v. | |
| constexpr | Vec (T a) |
| Construct a vector with all elements set to a. | |
| constexpr | Vec (T x, T y, T z) |
| Construct a vector with elements (x, y, z). | |
| template<typename U> | |
| constexpr | Vec (Vec< U, 2 > xy, T z) |
| Construct a vector with (x, y) taken from the 2D vector xy, and z as the final element. | |
| self_t | abs () const |
| Element-wise absolute value. | |
| self_t | add (const self_t &v) const |
| Vector addition. | |
| self_t | add (const self_t &v) const |
| Vector addition. | |
| self_t | add (const self_t &v) const |
| Vector addition. | |
| Vec< T, 3 > | add (T dx, T dy, T dz) const |
| self_t | align (const self_t &from, const self_t &to) const |
| Apply a rotation to this which aligns the unit vectors from with to. | |
| self_t | align (const self_t &from, const self_t &to) const |
| Apply a rotation to this which aligns the unit vectors from with to. | |
| Vec< T, 3 > | align (const Vec< T, 3 > &from, const Vec< T, 3 > &to) |
| T | angle_to (const self_t &v) const |
| Angle between vectors. | |
| T | angle_to (const self_t &v) const |
| Angle between vectors. | |
| index_t | argmax () const |
| Return the index of the coordinate with the largest absolute value. | |
| index_t | argmin () const |
| Return the index of the coordinate with the smallest absolute value. | |
| T * | begin () |
| const T * | begin () const |
| self_t | bounce_on (const self_t &normal) const |
| Elastic collision. | |
| self_t | bounce_on (const self_t &normal) const |
| Elastic collision. | |
| self_t | ceil () const |
| Element-wise ceiling function. | |
| self_t | clamp (const self_t &lo, const self_t &hi) const |
| Element-wise clamp. | |
| self_t | clamp (const self_t &lo, const self_t &hi) const |
| Element-wise clamp. | |
| Vec< T, 3 > | cross (Vec< T, 3 > v) const |
| T | dist (const self_t &pt) const |
| Distance between points. | |
| T | dist (const self_t &pt) const |
| Distance between points. | |
| T | dist2 (const self_t &pt) const |
| Distance squared to a point. | |
| T | dist2 (const self_t &pt) const |
| Distance squared to a point. | |
| T | dot (const self_t &v) const |
| Dot product. | |
| T | dot (const self_t &v) const |
| Dot product. | |
| T | dot (const self_t &v) const |
| Dot product. | |
| T | dot (T xx, T yy, T zz) const |
| T * | end () |
| const T * | end () const |
| self_t | floor () const |
| Element-wise floor function. | |
| T | fraction_on (const self_t &axis) const |
| Return the component of this that projects to axis, as a fraction of axis's length. | |
| T | fraction_on (const self_t &axis) const |
| Return the component of this that projects to axis, as a fraction of axis's length. | |
| T & | get (index_t idx) |
| const T & | get (index_t idx) const |
| bool | is_finite_real () const |
| bool | is_zero () const |
| Return true if all elements are zero. | |
| T | mag () const |
| Euclidean norm (magnitude). | |
| T | mag2 () const |
| Squared magnitude. | |
| T | max () const |
| Maximum element. | |
| self_t | max (const self_t &v) const |
| Element-wise maximum of two Vecs. | |
| self_t | max (const self_t &v) const |
| Element-wise maximum of two Vecs. | |
| T | min () const |
| Minimum element. | |
| self_t | min (const self_t &v) const |
| Element-wise minimum of two Vecs. | |
| self_t | min (const self_t &v) const |
| Element-wise minimum of two Vecs. | |
| self_t | mix (const self_t &v, T mix) const |
| Linear interpolation. | |
| self_t | mix (const self_t &v, T mix) const |
| Linear interpolation. | |
| operator Vec< U, N > () const | |
| Element typecast. | |
| bool | operator!= (const self_t &vv) const |
| Inequality test. | |
| bool | operator!= (const self_t &vv) const |
| Inequality test. | |
| self_t & | operator*= (const self_t &vv) |
| Element-wise multiplication and assignment. | |
| self_t & | operator*= (T s) |
| Scalar multiplication and assignment. | |
| self_t | operator+ (const self_t &v) const |
| Element-wise addition. | |
| self_t | operator+ (const self_t &v) const |
| Element-wise addition. | |
| self_t & | operator+= (const self_t &vv) |
| Element-wise addition and assignment. | |
| self_t & | operator+= (const self_t &vv) |
| Element-wise addition and assignment. | |
| self_t | operator- () const |
| Negation. | |
| self_t | operator- (const self_t &v) const |
| Element-wise subtraction. | |
| self_t | operator- (const self_t &v) const |
| Element-wise subtraction. | |
| self_t & | operator-= (const self_t &vv) |
| Subtraction and assignment. | |
| self_t & | operator-= (const self_t &vv) |
| Subtraction and assignment. | |
| self_t & | operator/= (T s) |
| Scalar division and assignment. | |
| bool | operator== (const self_t &vv) const |
| Equality test. | |
| bool | operator== (const self_t &vv) const |
| Equality test. | |
| T & | operator[] (index_t idx) |
| Vector element access. | |
| const T & | operator[] (index_t idx) const |
| Vector element access. | |
| Vec< T, 3 > | operator^ (Vec< T, 3 > v) const |
| Vector cross product. | |
| T | product () const |
| Multiply all elements together. | |
| self_t | project_on (const self_t &axis) const |
| Orthogonal projection to an axis. | |
| self_t | project_on (const self_t &axis) const |
| Orthogonal projection to an axis. | |
| self_t | reflect_about (self_t normal) const |
| Reflection about a normal. | |
| self_t | reflect_about (self_t normal) const |
| Reflection about a normal. | |
| Vec< T, 3 > | reflected_x () const |
| Vec< T, 3 > | reflected_y () const |
| Vec< T, 3 > | reflected_z () const |
| PointType< T, M >::point_t | resized () const |
| Resized copy of a vector. | |
| Vec< T, 3 > | rotate (T u, T v, T w, T a, T b, T c, T radians) |
| Vec< T, 3 > | rotate (T u, T v, T w, T radians) const |
| Vec< T, 3 > | rotate (Vec< T, 3 > axis, T radians) const |
| Vec< T, 3 > | rotate (Vec< T, 3 > axis, Vec< T, 3 > center, T radians) |
| self_t | round () const |
| Round each element to the nearest integer. | |
| self_t | scale (const self_t &v) const |
| Element-wise multiplication. | |
| self_t | scale (const self_t &v) const |
| Element-wise multiplication. | |
| self_t | scale (const self_t &v) const |
| Element-wise multiplication. | |
| self_t | scale (T a) const |
| Scalar multiple. | |
| Vec< T, 3 > | scale (T a, T b, T c) const |
| index_t | size () const |
| The number of elements in this vector. Always equal to N. | |
| self_t | sub (const self_t &v) const |
| Vector subtraction. | |
| self_t | sub (const self_t &v) const |
| Vector subtraction. | |
| self_t | sub (const self_t &v) const |
| Vector subtraction. | |
| Vec< T, 3 > | sub (T dx, T dy, T dz) const |
| T | sum () const |
| Sum the elements of the vector. | |
| Vec< T, 3 > | to_spherical () const |
| self_t | unit () const |
| Vector normalization. | |
| self_t | with_length (T mag) const |
| Compute a vector with the direction of this and a new magnitude mag. | |
Static Public Member Functions | |
| static Vec< T, 3 > | from_spherical (T r, T polar, T azi) |
Static Public Attributes | |
| static constexpr index_t | N |
| The dimension of this object. | |
| static const self_t | ones |
| static const self_t | unit_x |
| static const Vec< T, 3 > | X_AXIS |
| (1, 0, 0) constant | |
| static const Vec< T, 3 > | Y_AXIS |
| (0, 1, 0) constant | |
| static const Vec< T, 3 > | Z_AXIS |
| (0, 0, 1) constant | |
| static const self_t | zeros |
Protected Attributes | |
| T | v [N] |
Related Symbols | |
(Note that these are not member symbols.) | |
| geom::Vec< T, N > | abs (const geom::Vec< T, N > &v) |
| geom::Vec< T, N > | ceil (const geom::Vec< T, N > &v) |
| geom::Vec< T, N > | cos (const geom::Vec< T, N > &v) |
| geom::Vec< T, N > | exp (const geom::Vec< T, N > &v) |
| geom::Vec< T, N > | floor (const geom::Vec< T, N > &v) |
| geom::Vec< T, N > | log (const geom::Vec< T, N > &v) |
| geom::Vec< T, N > | max (const geom::Vec< T, N > &a, const geom::Vec< T, N > &b) |
| geom::Vec< T, N > | min (const geom::Vec< T, N > &a, const geom::Vec< T, N > &b) |
| const Vec< T, N > | operator* (const Vec< T, N > &a, const Vec< T, N > &b) |
| Vec< T, N > | operator* (const Vec< T, N > &v, U d) |
| Vec< T, N > | operator* (U d, const Vec< T, N > &v) |
| const Vec< T, N > | operator/ (const Vec< T, N > &a, const Vec< T, N > &b) |
| Vec< T, N > | operator/ (const Vec< T, N > &v, U d) |
| Vec< T, N > | operator/ (const Vec< T, N > &v, U d) |
| geom::Vec< T, N > | sin (const geom::Vec< T, N > &v) |
| geom::Vec< T, N > | sqrt (const geom::Vec< T, N > &v) |
| geom::Vec< T, N > | tan (const geom::Vec< T, N > &v) |
Detailed Description
class geom::Vec< T, 3 >
3D specialization of vector class.
Vec<T,3>'s elements may be accessed under these equivalent naming schemes:
v.{x,y,z} // conventional Euclidean coordinate names
v.{s,t,u} // conventional parameterization coordinate names
v.{r,g,b} // conventional color tuple coordinate names
x, s, and r all refer to the same element.
Member Typedef Documentation
◆ point_t
| using point_t |
The type of a point in this object's space.
An N-vector of T if N > 1, otherwise a T.
Member Function Documentation
◆ abs()
|
inline |
Element-wise absolute value.
- Returns
- A new vector x such that x[i] = abs(this[i]).
◆ add() [1/4]
Vector addition.
- Parameters
-
v Another vector.
- Returns
- A new vector x such that x[i] = this[i] + v[i].
◆ add() [2/4]
Vector addition.
- Parameters
-
v Another vector.
- Returns
- A new vector x such that x[i] = this[i] + v[i].
◆ add() [3/4]
Vector addition.
- Parameters
-
v Another vector.
- Returns
- A new vector x such that x[i] = this[i] + v[i].
◆ add() [4/4]
|
inline |
- Returns
- (dx, dy, dz) added with this
◆ align()
Compute a transform aligning from with to and apply it to this.
◆ angle_to() [1/2]
Angle between vectors.
- Parameters
-
v Another vector.
- Returns
- Angle in radians between this and v, between 0 and pi.
◆ angle_to() [2/2]
|
inline |
Angle between vectors.
- Parameters
-
v Another vector.
- Returns
- Angle in radians between this and v, between 0 and pi.
◆ begin() [1/2]
|
inline |
- Returns
- A writeable iterator pointing at the first element.
◆ begin() [2/2]
|
inline |
- Returns
- A read-only iterator pointing at the first element.
◆ bounce_on() [1/2]
Elastic collision.
Treat this as a velocity vector or incident ray; this function returns the velocity reflected off of a surface with normal normal. Convenience for -reflect_about(normal).
- Parameters
-
normal Normal of surface to "bounce" on.
- Returns
- The "bounced" direction vector.
◆ bounce_on() [2/2]
Elastic collision.
Treat this as a velocity vector or incident ray; this function returns the velocity reflected off of a surface with normal normal. Convenience for -reflect_about(normal).
- Parameters
-
normal Normal of surface to "bounce" on.
- Returns
- The "bounced" direction vector.
◆ ceil()
|
inline |
Element-wise ceiling function.
- Returns
- A new vector x such that x[i] = ceil(this[i]).
◆ clamp() [1/2]
Element-wise clamp.
- Parameters
-
lo Element-wise lower extremes. hi Element-wise upper extremes.
- Returns
- A new vector such that each element x[i] is clamped between lo[i] and hi[i].
◆ clamp() [2/2]
Element-wise clamp.
- Parameters
-
lo Element-wise lower extremes. hi Element-wise upper extremes.
- Returns
- A new vector such that each element x[i] is clamped between lo[i] and hi[i].
◆ cross()
- Returns
- Cross product of this by v, in the order shown.
◆ dist() [1/2]
Distance between points.
- Parameters
-
pt Another point.
- Returns
- The distance between this and pt.
◆ dist() [2/2]
|
inline |
Distance between points.
- Parameters
-
pt Another point.
- Returns
- The distance between this and pt.
◆ dist2() [1/2]
Distance squared to a point.
- Parameters
-
pt Another point.
- Returns
- The square of the distance between this and pt.
◆ dist2() [2/2]
|
inline |
Distance squared to a point.
- Parameters
-
pt Another point.
- Returns
- The square of the distance between this and pt.
◆ dot() [1/4]
Dot product.
- Parameters
-
v Another vector.
- Returns
- The dot product of this with v.
◆ dot() [2/4]
|
inline |
Dot product.
- Parameters
-
v Another vector.
- Returns
- The dot product of this with v.
◆ dot() [3/4]
|
inline |
Dot product.
- Parameters
-
v Another vector.
- Returns
- The dot product of this with v.
◆ dot() [4/4]
|
inline |
- Returns
- Dot product of this with the vector (xx, yy, zz)
◆ end() [1/2]
|
inline |
- Returns
- A writeable iterator pointing just beyond the last element.
◆ end() [2/2]
|
inline |
- Returns
- A read-only iterator pointing just beyond the last element.
◆ floor()
|
inline |
Element-wise floor function.
- Returns
- A new vector x such that x[i] = floor(this[i]).
◆ fraction_on() [1/2]
|
inlineinherited |
Return the component of this that projects to axis, as a fraction of axis's length.
- Parameters
-
axis An arbitrary basis vector.
◆ fraction_on() [2/2]
|
inline |
Return the component of this that projects to axis, as a fraction of axis's length.
- Parameters
-
axis An arbitrary basis vector.
◆ from_spherical()
|
inlinestatic |
Construct a point from spherical coordinates (r, polar, azimuth), to euclidean coordinates, where r is the radius, polar is the angle from the +z axis, and azimuth is the angle about z+ from the x+ axis.
- Returns
- A euclidean point constructed from spherical coordinates.
◆ get() [1/2]
|
inline |
Get the element at index idx.
- Parameters
-
idx Index of element.
- Returns
- A reference to the element at idx.
◆ get() [2/2]
|
inline |
Get the element at index idx.
- Parameters
-
idx Index of element.
- Returns
- A const reference to the element at idx.
◆ is_finite_real()
|
inline |
- Returns
- true if no elements are an infinity or NaN.
◆ mag()
|
inline |
Euclidean norm (magnitude).
- Returns
- The Euclidean magnitude (geometric length) of this vector.
◆ mag2()
|
inline |
Squared magnitude.
- Returns
- The square of the magnitude of this vector.
◆ max() [1/3]
|
inlineinherited |
Maximum element.
- Returns
- The value of the component with the highest value.
◆ max() [2/3]
Element-wise maximum of two Vecs.
- Parameters
-
v Another vector.
- Returns
- A new vector x such that x[i] = max(this[i], v[i]).
◆ max() [3/3]
Element-wise maximum of two Vecs.
- Parameters
-
v Another vector.
- Returns
- A new vector x such that x[i] = max(this[i], v[i]).
◆ min() [1/3]
|
inlineinherited |
Minimum element.
- Returns
- The value of the component with the lowest value.
◆ min() [2/3]
Element-wise minimum of two Vecs.
- Parameters
-
v Another vector.
- Returns
- A new vector x such that x[i] = min(this[i], v[i]).
◆ min() [3/3]
Element-wise minimum of two Vecs.
- Parameters
-
v Another vector.
- Returns
- A new vector x such that x[i] = min(this[i], v[i]).
◆ mix() [1/2]
Linear interpolation.
A mix parameter of 0 evaluates to this, while 1 is v.
- Parameters
-
v Another vector. mix A mixing factor between 0 and 1.
- Returns
- A linear mixing of this with v.
◆ mix() [2/2]
Linear interpolation.
A mix parameter of 0 evaluates to this, while 1 is v.
- Parameters
-
v Another vector. mix A mixing factor between 0 and 1.
- Returns
- A linear mixing of this with v.
◆ operator Vec< U, N >()
Element typecast.
- Returns
- A new vector with all elements cast to type U.
◆ operator!=() [1/2]
|
inlineinherited |
Inequality test.
- Returns
- true if any corresponding elements of this and vv are unequal, false otherwise.
◆ operator!=() [2/2]
|
inline |
Inequality test.
- Returns
- true if any corresponding elements of this and vv are unequal, false otherwise.
◆ operator-()
|
inlineinherited |
Negation.
- Returns
- A copy of this vector with all elements negated (i.e. a vector pointing in the opposite direction).
◆ operator==() [1/2]
|
inlineinherited |
Equality test.
- Returns
- true if all corresponding elements of this and vv are equal, false otherwise.
◆ operator==() [2/2]
|
inline |
Equality test.
- Returns
- true if all corresponding elements of this and vv are equal, false otherwise.
◆ operator[]() [1/2]
|
inlineinherited |
Vector element access.
- Parameters
-
idx Index of element to retrieve.
- Returns
- A reference to the element at index idx.
◆ operator[]() [2/2]
|
inline |
Vector element access.
- Parameters
-
idx Index of element to retrieve.
- Returns
- A read-only reference to the element at index idx.
◆ project_on() [1/2]
|
inlineinherited |
Orthogonal projection to an axis.
- Parameters
-
axis A direction vector.
- Returns
- A vector in direction axis with magnitude equal to the component of this aligned with axis.
◆ project_on() [2/2]
Orthogonal projection to an axis.
- Parameters
-
axis A direction vector.
- Returns
- A vector in direction axis with magnitude equal to the component of this aligned with axis.
◆ reflect_about() [1/2]
|
inlineinherited |
Reflection about a normal.
- Parameters
-
normal Axis of reflection.
- Returns
- A copy of this vector reflected across the given axis.
◆ reflect_about() [2/2]
Reflection about a normal.
- Parameters
-
normal Axis of reflection.
- Returns
- A copy of this vector reflected across the given axis.
◆ reflected_x()
|
inline |
- Returns
- A copy with the X component negated
◆ reflected_y()
|
inline |
- Returns
- A copy with the Y component negated
◆ reflected_z()
|
inline |
- Returns
- A copy with the Z component negated
◆ resized()
◆ rotate() [1/4]
|
inline |
- Returns
- A copy of this vector rotated by angle radians about the axis (u, v, w), and centerpoint (a, b, c).
◆ rotate() [2/4]
|
inline |
- Returns
- A copy of this vector rotated by angle radians about the axis (u, v, w).
◆ rotate() [3/4]
- Returns
- A copy of this vector rotated by angle radians about axis.
◆ rotate() [4/4]
- Returns
- A copy of this vector rotated by angle radians about rotation axis axis and centerpoint center.
◆ scale() [1/5]
Element-wise multiplication.
- Parameters
-
v Another vector.
- Returns
- A new vector x such that x[i] = this[i] * v[i].
◆ scale() [2/5]
Element-wise multiplication.
- Parameters
-
v Another vector.
- Returns
- A new vector x such that x[i] = this[i] * v[i].
◆ scale() [3/5]
Element-wise multiplication.
- Parameters
-
v Another vector.
- Returns
- A new vector x such that x[i] = this[i] * v[i].
◆ scale() [4/5]
|
inline |
Scalar multiple.
- Parameters
-
a A constant scale factor.
- Returns
- A new vector x such that x[i] = this[i] * a.
◆ scale() [5/5]
|
inline |
- Returns
- Element-wise scaled copy
◆ sub() [1/4]
Vector subtraction.
- Parameters
-
v Another vector.
- Returns
- A new vector x such that x[i] = this[i] - v[i].
◆ sub() [2/4]
Vector subtraction.
- Parameters
-
v Another vector.
- Returns
- A new vector x such that x[i] = this[i] - v[i].
◆ sub() [3/4]
Vector subtraction.
- Parameters
-
v Another vector.
- Returns
- A new vector x such that x[i] = this[i] - v[i].
◆ sub() [4/4]
|
inline |
- Returns
- (dx, dy, dz) subtracted from this
◆ to_spherical()
|
inline |
Convert this euclidean point to spherical coordinates (r, polar, azimuth), with both angles in radians. Polar angle is the angle from the +z axis in the range (0, pi), and azimuth is the angle about +z from the +x axis in the range (-pi, pi).
- Returns
- This euclidean point converted to spherical coordinates.
◆ unit()
|
inline |
Vector normalization.
- Returns
- A copy of this vector with unit length.
◆ with_length()
|
inline |
Compute a vector with the direction of this and a new magnitude mag.
If this is the zero vector, it will remain unchanged.
Friends And Related Symbol Documentation
◆ abs()
◆ ceil()
◆ cos()
◆ exp()
◆ floor()
◆ log()
◆ max()
Element-wise maximum.
◆ min()
Element-wise minimum.
◆ operator*() [1/3]
Element-wise vector multiplication
- Parameters
-
a A vector b A vector
- Returns
- A new vector x such that x[i] = a[i] * b[i]
◆ operator*() [2/3]
Vector-scalar multiplication
- Parameters
-
v A vector d Scalar value of type satisfying std::is_scalar
- Returns
- A new vector x such that x[i] = v[i] * d
◆ operator*() [3/3]
Vector-scalar multiplication
- Parameters
-
d Scalar value of type satisfying std::is_scalar v A vector
- Returns
- A new vector x such that x[i] = d * v[i]
◆ operator/() [1/3]
Element-wise vector division
- Parameters
-
a A vector b A vector
- Returns
- A new vector x such that x[i] = a[i] / b[i]
◆ operator/() [2/3]
Scalar division by a vector
- Parameters
-
d Scalar value v A vector
- Returns
- A new vector x such that x[i] = d / v[i]
◆ operator/() [3/3]
Vector division by a scalar
- Parameters
-
v A vector d Scalar value
- Returns
- A new vector x such that x[i] = v[i] / d
◆ sin()
◆ sqrt()
◆ tan()
The documentation for this class was generated from the following files:
Generated on for geomc by